Slides
A pdf version of the slides, linking to here.
Latest version is here
From
http://www.ics.uci.edu/~eppstein/junkyard/all.html I found this nice page (sadly a dead link now)
http://britton.disted.camosun.bc.ca/jbconics.htm
Conics
Circle
Centered at
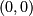
with radius r.
Ellipse
Centered at
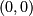
, semi x-axis length is a, semi y-axis length is b.
Parabola
Centered at
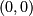
, distance from the vertex to the focus is a.
Hyperbola
Centered at
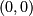
, vertices are
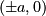
and the asymptotes are
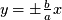
.
Foci properties
There are lots of these, we'll focus on the most straightforward ones, foci are on the real axis. ELI5.
Circle
Just the center and radius description. Easy peasy!
Ellipse
The pin-and-string description. Foci at
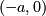
and
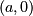
. Sum of the distances to the two foci is fixed.
Parabola
Distance equals width. Foci at a, vertical line through
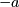
. The distance to the foci is equal to the horizontal distance to the line.
Hyperbola.
Like an ellipse, but difference instead of sum. The difference of the distances to the two foci is fixed.
Using the idea that
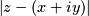
is the distance from z to
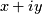
.
Circle
Centered at
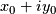
with radius r.
Ellipse
Centered at
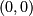
, foci at
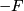
and
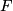
, sum of distances is c.
Parabola
Centered at
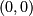
, foci at
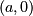
. Trick is we want the real part of
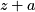
, which is
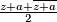
which equals
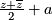
.
Hyperbola
Centered at
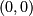
, foci at
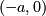
and
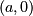
, constant difference is d.
There are multiple possibilities, but here are the common ones.
Circle
Ellipse
Parabola
Hyperbola
All conics can be written in this generic form, but I think that is above where we need to go.
Tests on the coefficients determine what sort of conic it is.
Some problems to warm up in week 1
- What is the ellipse form of a circle centered at
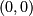 with radius r?
with radius r?
- Lets work out the slope of tangent lines of a circle.
- Make y the subject, making it a function by taking the positive square root, then differentiate. Which part of the circle is this?
- Same as before, but grab the other side of the circle.
- Now for a trick. Pretend y is shorthand for a function. This trick is called implicit differentiation. Now use the chain rule to show
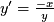 .
.
- What is the slope of the lines perpendicular to those tangent lines?
- Sketch one on a circle graph. Where do those perpendicular (normal) lines always go through?
- It appears that the hyperbola tries to reach the asymptotes.
- Rewrite the hyperbola form in the form
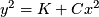 , clearly identify C and K in terms of a and b.
, clearly identify C and K in terms of a and b.
- As
 gets large, the K term gets swamped, so we have
gets large, the K term gets swamped, so we have 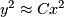 . Assume they are actually equal, and solve to get the two asymptotes.
. Assume they are actually equal, and solve to get the two asymptotes.
- Sliding shapes is pretty easy, moving
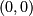 to
to 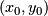 only requires replacing x with
only requires replacing x with 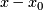 and y with
and y with 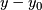
- Write the forms for each conic (ellipse, parabola and hyperbola) with the new center
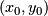 .
.
- Use sliding to explain why
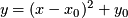 is the
is the 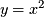 graph moved so the turning point is
graph moved so the turning point is 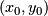 , and use calculus to check this is true.
, and use calculus to check this is true.
- These are all conics, use algebra to identify which type it is and the relevant details.
-
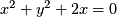 (not centered at
(not centered at 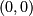 )
)
-
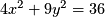
-
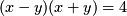
-
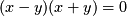 this isn't a proper conic, but it is familiar and is technically a degenerate conic.
this isn't a proper conic, but it is familiar and is technically a degenerate conic.
![\begin{tikzpicture} \draw[gray, very thin] (-3.1,-3.1) grid (3.1,3.1); \draw[red,<->] (-3.2, 0) -- (3.2,0); \draw[red,<->] (0,-3.2) -- (0,3.2); \draw[blue] plot[variable=\t,samples=1000,domain=0:360] ({cos(\t)},{sin(\t)}); \end{tikzpicture}](/foswiki/pub/Main/NceaConics/latex12086c4347a2a1159609a88e4fa8f57d.png)
![\begin{tikzpicture} \draw[gray, very thin] (-3.1,-3.1) grid (3.1,3.1); \draw[red,<->] (-3.2, 0) -- (3.2,0); \draw[red,<->] (0,-3.2) -- (0,3.2); \draw[blue] plot[blue,variable=\t,samples=1000,domain=0:360] ({2*cos(\t)},{sin(\t)}); \end{tikzpicture}](/foswiki/pub/Main/NceaConics/latex80e646090614b45132b015cc71d2b7cd.png)
![\begin{tikzpicture} \draw[gray, very thin] (-3.1,-3.1) grid (3.1,3.1); \draw[red,<->] (-3.2, 0) -- (3.2,0); \draw[red,<->] (0,-3.2) -- (0,3.2); \draw[blue] plot[variable=\t,samples=1000,domain=0:1.4] ({(\t)^2},{2*\t}); \draw[blue] plot[variable=\t,samples=1000,domain=0:1.4] ({(\t)^2},{-2*\t}); \draw[dotted] (-1,3) -- (-1,-3); \end{tikzpicture}](/foswiki/pub/Main/NceaConics/latexf722b2eeb2ef6e820d8be376e904c6b4.png)
![\begin{tikzpicture} \draw[gray, very thin] (-3.1,-3.1) grid (3.1,3.1); \draw[red,<->] (-3.2, 0) -- (3.2,0); \draw[red,<->] (0,-3.2) -- (0,3.2); \draw[blue] plot[variable=\t,samples=1000,domain=-70:70] ({sec(\t)},{tan(\t)}); \draw[blue] plot[variable=\t,samples=1000,domain=-70:70] ({-sec(\t)},{tan(\t)}); \draw[dotted] (3,3) -- (-3,-3); \draw[dotted] (-3,3) -- (3,-3); \end{tikzpicture}](/foswiki/pub/Main/NceaConics/latex0134f1c04e06c60ee3710dbbaa4e6744.png)
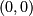 with radius r?
with radius r?
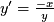 .
.
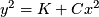 , clearly identify C and K in terms of a and b.
, clearly identify C and K in terms of a and b.
 gets large, the K term gets swamped, so we have
gets large, the K term gets swamped, so we have 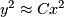 . Assume they are actually equal, and solve to get the two asymptotes.
. Assume they are actually equal, and solve to get the two asymptotes.
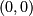 to
to 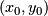 only requires replacing x with
only requires replacing x with 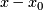 and y with
and y with 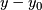
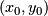 .
.
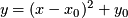 is the
is the 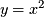 graph moved so the turning point is
graph moved so the turning point is 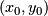 , and use calculus to check this is true.
, and use calculus to check this is true.
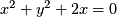 (not centered at
(not centered at 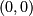 )
)
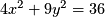
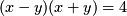
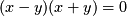 this isn't a proper conic, but it is familiar and is technically a degenerate conic.
this isn't a proper conic, but it is familiar and is technically a degenerate conic.


